Dimension of the Feature Space¶
The features implemented in the mlmd are the Structural Information Fiter Features (SIFF). The SIFF method produces a feature vector per structure for energy calculations. The dimension of the feature space is the result of encoding the information of the composition, and geometry of a structure. The image at the top of the page shows the process of building a feature vector for the structure displayed in part A) of the image.
The Feature Space in the Structural Information Fiter Features¶
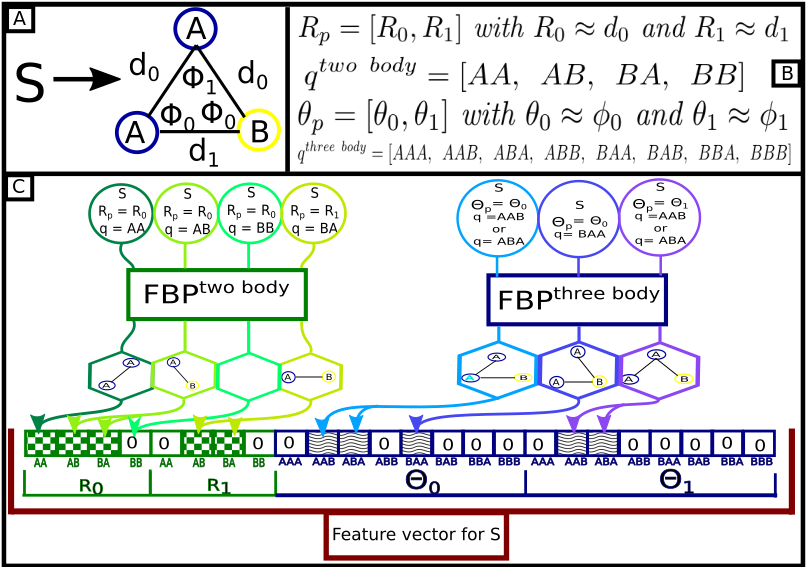
A) The S structure with three atoms, of two different species A and B, the distances between the atoms are either \({\textit{d}_0}\) or \({\textit{d}_1}\), the angles are \({\Phi_0}\) or \({\Phi_1}\). B) The parameters for the SIFF calculations, \({\textit{R}_p}\) is the center of the Gaussian part of the SIFF two body, it selects (filters) which interatomic distances are accounted for a given feature, here it can have two values \({\textit{R}_0}\) or \({\textit{R}_1}\), the \({\textit{q}^{two-body}}\) bodyis the set of all the two body combinations of the species in the system. \({\theta_p}\) is the center of the Gaussian part of the SIFF three body, it selects (filters) which trios of particles are taken into account in a given feature, the \({\textit{q}^{three-body}}\) is the set of all the three body combinations of the species in the system. C) Scheme of the feature vector calculation, the circles represent the input needed to calculate an individual feature for the feature vector, in the case of the SIFF tow body, the input is: the structure, the value of \({\textit{R}_p}\) and the q interaction, in the case of the first feature (from left to right) \({\textit{R}_p}\) = \({\textit{R}_0}\) \({\approx}\) \({\textit{d}_0}\) and the q interaction is AA, with these parameters the output (represented in the hexagon) is the result of extracting (filtering) the geometrical parts of the structure that meet the parameters requirements, in the third example for SIFF two body, the input information is \({\textit{R}_p}\) = \({\textit{R}_0}\) \({\approx}\) \({\textit{d}_0}\) and the q interaction is BB, in this case, there are no geometrical part of the structure that meets the parameters, thus the output is empty. The three body feature calculation follows a similar process but instead of filtering the structure by interatomic distance, and two body combination, the selection process relies on the angle and the three body combination. Finally, the feature vector for the S structure is the concatenation of all the individual features. The dimension of the feature vector is the number of \({\textit{R}_p}\) values, times the number of \({\textit{q}^{two-body}}\) interactions, plus the number of \({\theta_p}\), times the number of \({\textit{q}^{two-body}}\) interactions. The checkboard and wavy pattern in the feature vector mark the features that are different from 0.
The fami_2b and fami_3b¶
The SIFF implemented in the mlmd package has some built-in filters (values for \({\textit{R}_p}\) and \({\theta_p}\)), there are 2-body filters and 3-body filters, the individual filters belong to families of filters, every family of filters have a certain number of filters equally spaced from an initial position to their respective cutoff (radius or angle). The 2-body families of filters are:
Family one has 15 filters (one every 0.3 A, from 1.0A to 5.2A)
fami_2b 1
Family tow (fami_2b 2) has 12 filters (one every 0.4 A, from 1.0A to 5.4A)
fami_2b 2
Family three has 10 filters (one every 0.5 A, from 1.0A to 5.5A)
fami_2b 3
Family four (fami_2b 4) has 8 filters (one every 0.6 A, from 1.0A to 5.2A)
fami_2b 4
The 3 body families of filters are:
Family one has 14 filters (one every [\({\pi}\) /15] rads , from 0 to \({\pi}\))
fami_3b 1
Family tow (fami_3b 2) has 9 filters (one every [\({\pi}\) /10] rads , from 0 to \({\pi}\))
fami_3b 2
Family three (fami_3b 3) has 7 filters (one every [\({\pi}\) /8] rads , from 0 to \({\pi}\))
fami_3b 3
Family three (fami_3b 4) has 6 filters (one every [\({\pi}\) /7] rads , from 0 to \({\pi}\))
fami_3b 4
Family three (fami_3b 5) has 5 filters (one every [\({\pi}\) /6] rads , from 0 to \({\pi}\))
fami_3b 5
Then, for example, a feature space for a system with 2 species, using family 2 for 2-body interactions, and families 3 and 4 for 3-body interactions, will have 152 features in total. The 2-body contribution will have 48 features, and the 3-body contribution will be 104 features. The 48 2-body features come from 4 interactions, and 12 filters in family 2 in 2-body interactions, then 4*12 = 48. The 104 comes from 8 3-body interactions, and families 3 and 4 have 7 and 6 filters respectively, then the number of 3-body filters is 13, then 8*13 = 104, finally 104 + 48 = 152 the total number of features.